When Do You Change Bounds On An Integral

Rather than expand one the given solution, I will demonstrate that why when we change variable via substitution we must besides change the bounds of integration:

Consider outset what an integral represents. The integral

# I = int_a^b \ f(10) \ dx #'

Is the same as the area under the curve #y=f(ten)# bound betwixt #x=a#, #10=b# and the #x#-axis.

Then now, allow us consider a physical case:

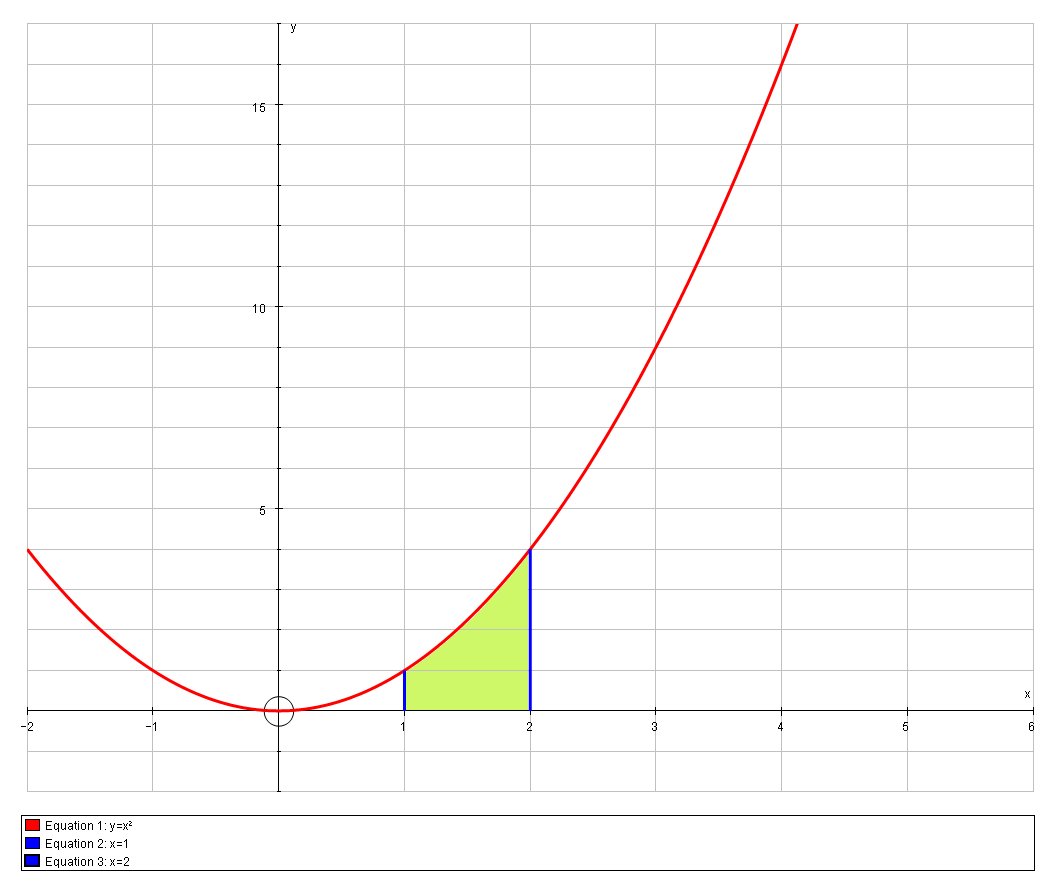
# I = int_1^two ten^2 \ dx #

Which is this expanse:

And, using our calculus of integration knowledge, we evaluate information technology as follows using the "ability rule":

# I = [ 10^3/3 ]_1^2#

# \ \ = 2^iii/three-ane^iii/3#

# \ \ = vii/3 #

At present, consider the post-obit integral:

# I = int_3^4 \ (ten-2)^ii \ dx #

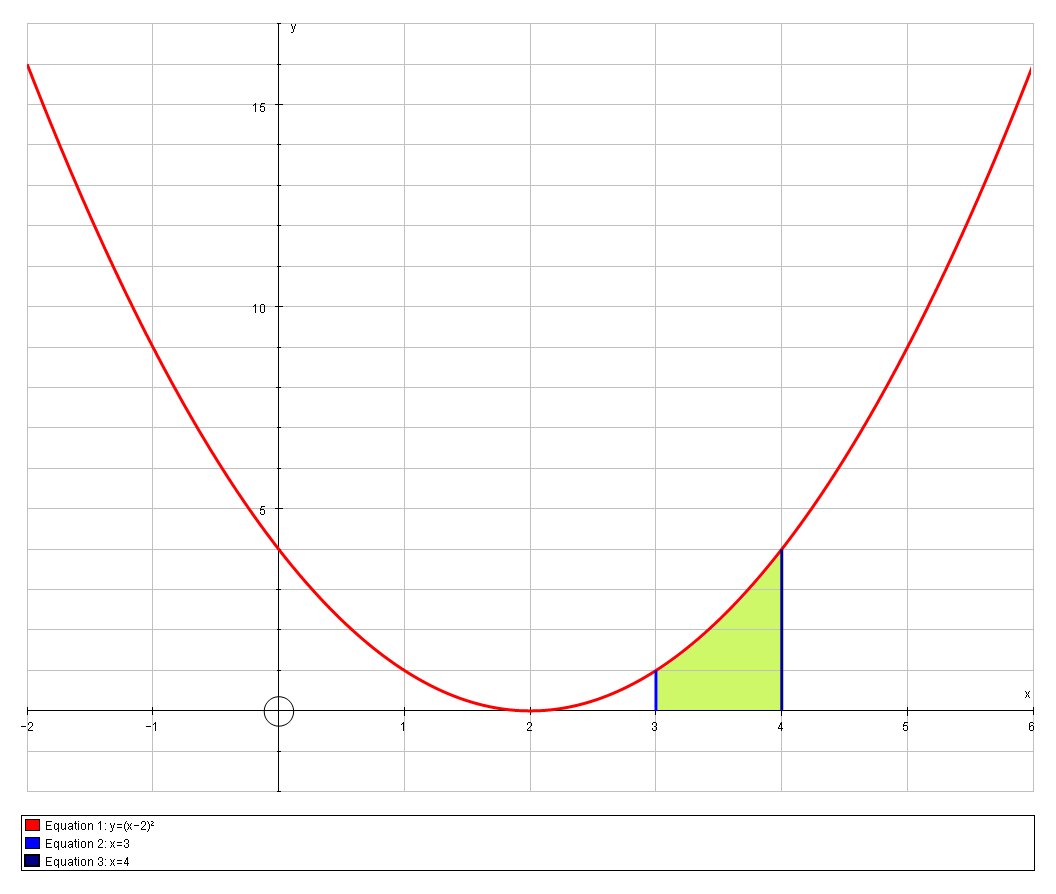
This is the same curve as above, but translated two units, and represents the same identical surface area equally above. We cannot utilize the integration power rule to this integrand "as is" and then we would typically (sometimes mentally) perform a substitution:

Let #u=x-2 => (du)/dx = 1#

And then if nosotros substitute and naively exit the limits of integration unchanged then we erroneously get:

# I = int_3^4 \ (x-2)^2 \ dx #
# \ \ = int_3^4 \ u^2 \ du #

# \ \ = [ u^3/3 ]_3^4 #

# \ \ = 4^iii/iii-three^3/3 #

# \ \ = 64/iii-27/3 #

# \ \ = 37/3 #

The reason this fails is because the the translation of the curve via a substitution requires a translation of the limits of integration from #10# to #u# via the relationship #u=x-2#, so the actual area nosotros but computed is as follows:

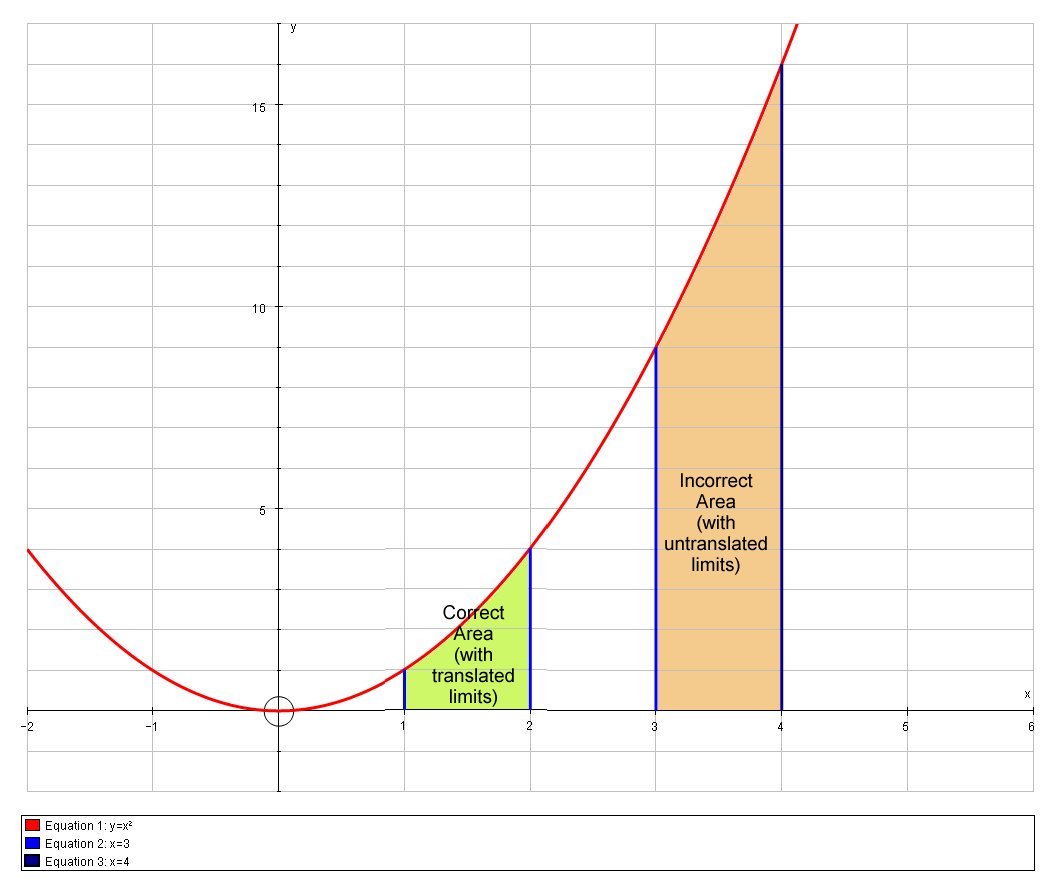
enter image source here
Wheres as when nosotros besides translate the limits of integration we get